Projects
On this page you can find a brief description of my current and past works, with links to the corresponding publications.
Current activities
Since early 2022, I am having the opportunity of extending my parallel mesh knowledges to high-order finite element methods.
Development of parallel unstructured hybrid mesh algorithms for high-order finite elements in AeroSol
I am focusing on developing data structures and algorithms for parallel unstructured meshes to be used for high-order continuous and discontinuous finite element methods. These are developed into a library that will be used by the AeroSol finite element software framework (more here and here).
Emphasis is put on the transparent management of parallel stencils for both continuous and discontinuous finite elements assembly. More details and some images are to come!
Recent activities
Not a long ago, I have been focusing for several years on developing robust methods and implementations for mesh adaptation in computational mechanics, particularly on parallel computing environments.
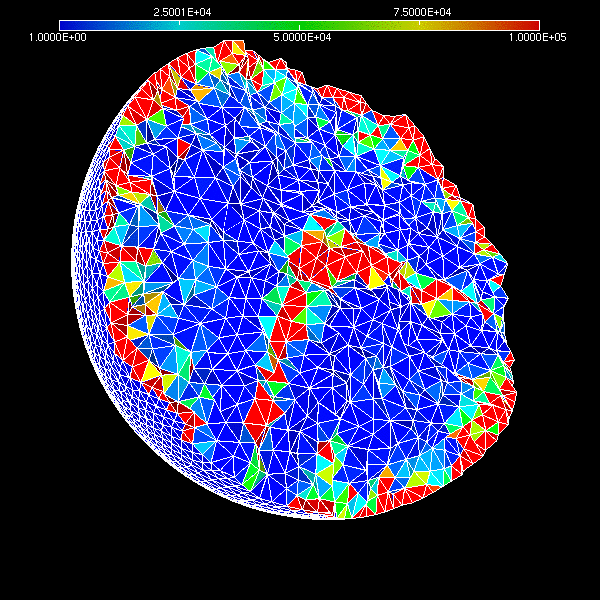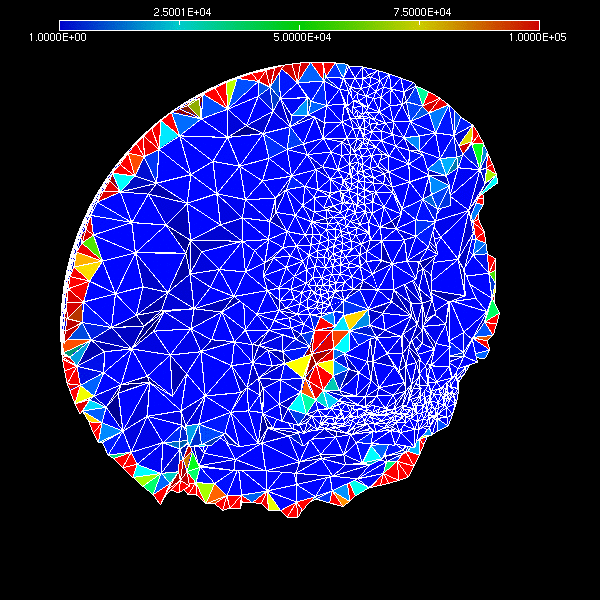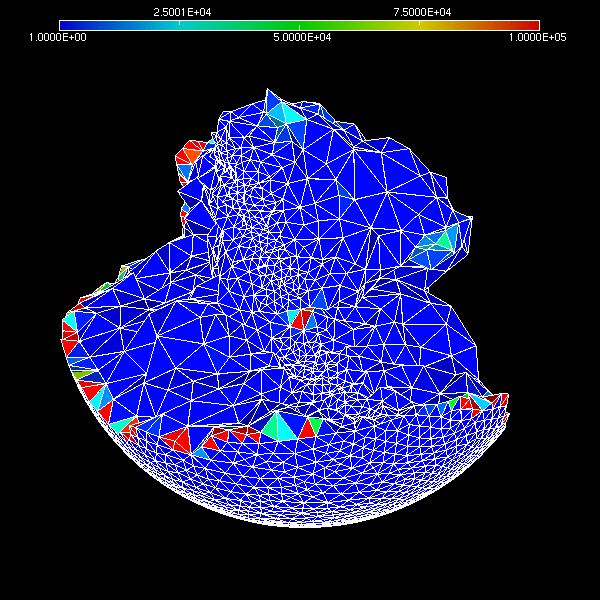
Development of the parallel mesh adaptation library ParMmg
ParMmg is an open source library for parallel mesh adaptation based on the serial Mmg remesher. Parallelism in mesh adaptation is needed whenever an adapted mesh becomes too large to be stored in the memory of a single computing node, or whenever a parallel solver needs to call a mesh adaptation procedure without introducing a computational bottleneck.
ParMmg (written in C using the MPI standard) targets three-dimensional unstructured meshes. Parallel adaptation is performed by iteratively remeshing each partition with Mmg (except on the parallel interfaces) and repartitioning the mesh in order to move unadapted zones to the interior of the partitions for the next iteration.
The aim is to produce a robust library that could support all the functionalities of the Mmg platform. ParMmg is currently developed for the ExaQUte and the MICROCARD European research projects.
I am currently maintaining the library together with Algiane Froehly. Details on the parallel remeshing algorithm can be found in:
- The conference paper (2021) Parallel unstructured mesh adaptation based on iterative remeshing and repartitioning, and the slides of the talk.
- The research report (2018) Parallel unstructured mesh adaptation using iterative remeshing and repartitioning.
Some recent reviews about the applications of Mmg to computational mechanics can also be found in:
- The preprint (2021) Tetrahedral remeshing in the context of large-scale numerical simulation and high performance computing.
- The preprint (2021) h– and r– adaptation on simplicial meshes using MMG tools.
Development of the constant-connectivity mesh adaptation library Fmg
Fmg is a library to perform constant-connectivity mesh adaptation (r-adaptation) in two and three dimensions for fluid mechanics simulations with moving fronts (like shock waves, free surface waves). R-adaptation can be particulary useful in conjunction with Arbitrary-Lagrangian Eulerian formulations of fluid flows, to ease the enforcement of conservation of flow quantities from the old to the adapted mesh.
I have developed the three-dimensional r-adaptation method and I am currently maintaining the library. Details on the algorithm can be found in:
- The journal paper (2021) Adaptive deformation of 3D unstructured meshes with curved body fitted boundaries with application to unsteady compressible flows.
- The conference paper (2019) R-adaptation for unsteady compressible flow simulations in three dimensions.
Past activities
My past activities have focused on the simulation of coupled problems (possibly with mesh adaptation) in computational mechanics.
Three-dimensional unsteady aeroelastic simulations with interpolation-free mesh adaptation
The simulation of transonic flutter phenomena, involving large displacements of an aileron behind an airplane wing, can still be tackled with body-fitted meshes by using remeshing during the time simulation. Conservative interpolation of flow quantities from the old to the adapted mesh is needed for an accurate determination of shock wave positions and aeroelastic stability limits. This has been performed during my PhD by means of the Mmg library coupled to an object oriented finite volume solver for compressible flow simulations, using an already well-developer interpolation-free approach allowing the conservation of flow quantities over adaptive meshes.
Detailed descriptions of the approach can be found in:
- My doctoral thesis (2018) Conservative interpolation-free mesh adaptation for three-dimensional aeroelastic simulations in unsteady compressible flows.
- The conference paper (2018) Numerical simulation of nonclassical aileron buzz over 3D unstructured adaptive meshes.
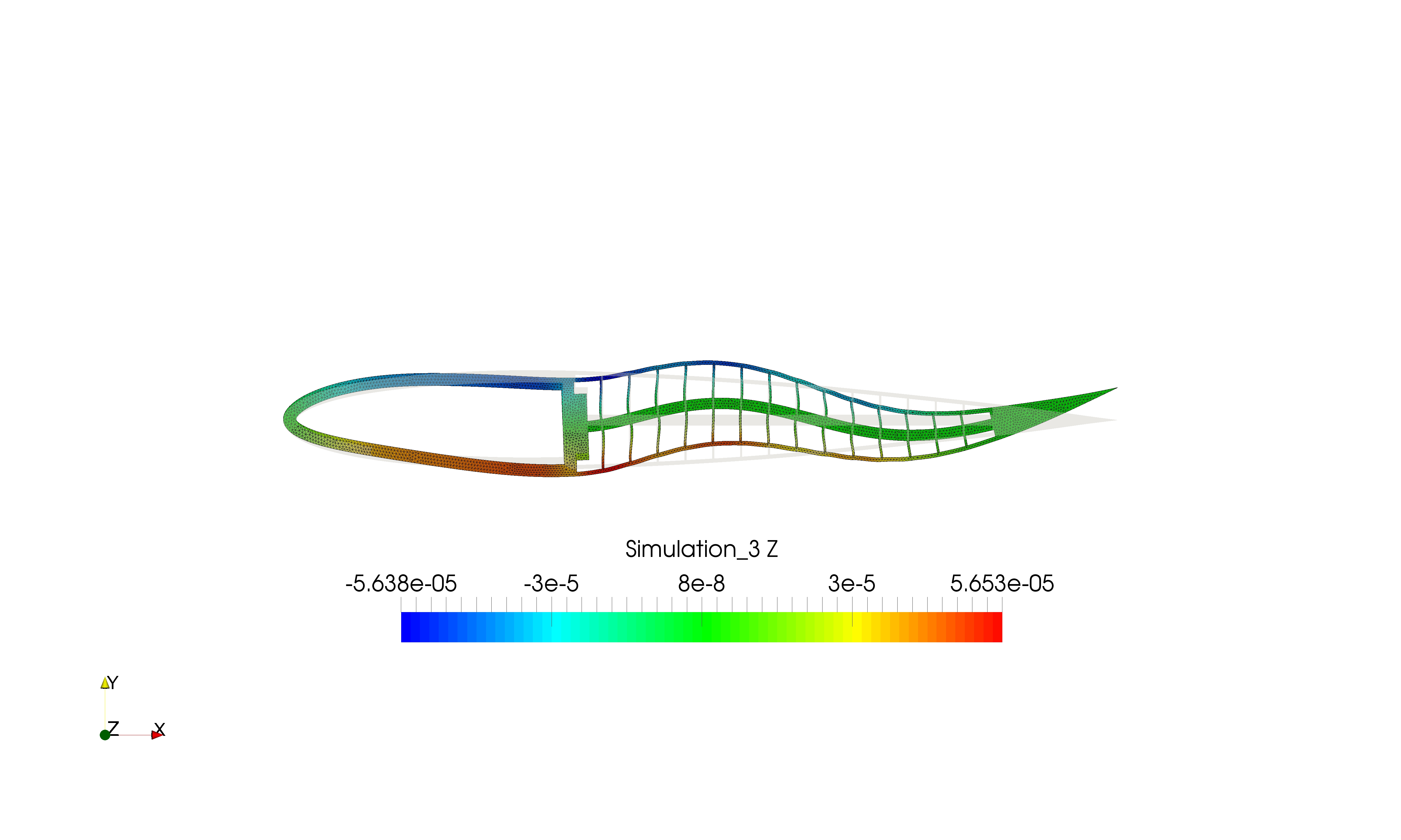
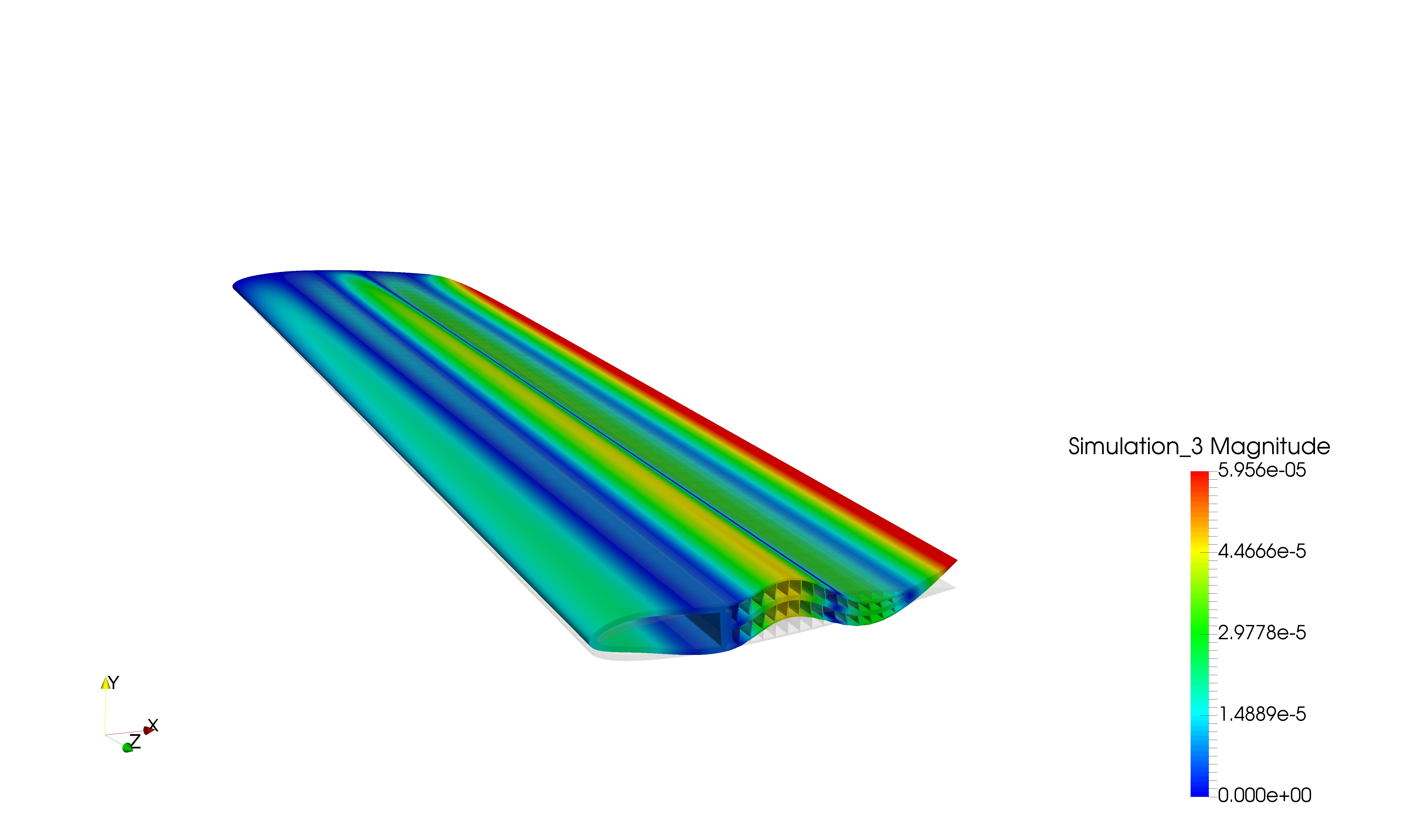
Generalized beam models for aeroelastic morphing analysis
The aeroelastic design of morphing helicopter blades requires fast computational models to be used to simulate a possibly large set of geometrical and material configurations. By resorting to the theory of generalized beam models, a reduced-order structural model has been derived during my PhD for the structural mechanics of slender helicopter blades made of composite materials.
Detailed descriptions can be found in:
- My doctoral thesis (2018) Conservative interpolation-free mesh adaptation for three-dimensional aeroelastic simulations in unsteady compressible flows.
- The conference paper (2018) Generalized beam models analysis for aeroelastic morphing applications.
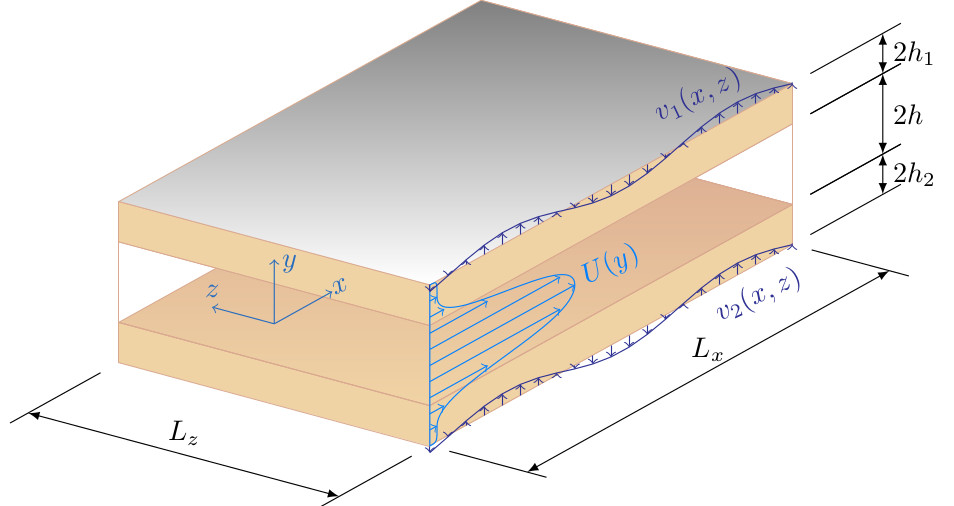
Simulation of optimal feedback control of plane channel flow over porous walls.
My very first approach to computational mechanics occurred with the development of a computational model for the optimal feedback control of the turbulent flow in a plane channel with porous walls.
The complete description can be found in my master thesis (2014) Optimal feedback control of plane channel flow over porous walls.
Acknowledgements
I warmly thank all the people I have, and I had, the chance to collaborate with.